Dziś zajmiemy się bryłami.
Temat: Bryły - ćwiczenia.
Podręcznik:
https://szaloneliczby.pl/bryly-sprawdzian-klasa-7/
Zadanie 1. (1pkt) Graniastosłup prawidłowy sześciokątny ma:
W podstawie jest sześciokąt, więc musimy dopasować odpowiedź.
Zadanie 2. (1pkt) W którym z tych prostopadłościanów zmieści się najmniej litrów wody?
Musimy w jednakowych jednostkach, najlepiej gdyby były to decymetry (wynik wyjdzie w litrach). Widać, że interesują nas dwie odpowiedzi B i D.
I tu kłania się czytanie ze zrozumieniem. Tłumaczyłem Wam, na lekcji, a sam policzyłem największą wartość :)
Jeszcze raz:
Odrzucamy B i D jako duże liczby w mnożeniu. Z "A" mamy 2*2=4 Porównując z "C' porównujemy dwie liczby: 2 i 1,5.
Zadanie 3. (1pkt) Jedną z różnic między prostopadłościanem, a sześcianem jest to, że:
Sześcian jest szczególnym prostopadłościanem. W sześcianie wszystkie ściany są kwadratami.
Zadanie 4. (1pkt) Objętość sześcianu, którego suma krawędzi jest równa 60cm wynosi:
Trzeba wiedzieć ile jest krawędzi. 60 : 12=
Ten wynik podnosimy do trzeciej potęgi.
Zadanie 5. (1pkt) Pole całkowite graniastosłupa, który powstanie z poniższej siatki jest równe:
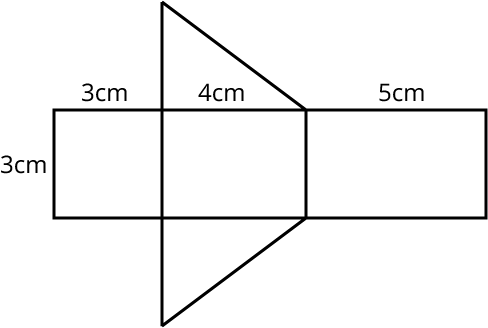

Trójkąt jest podstawą. To jednak nie jest kluczowa wiadomość, wystarczy zsumować powierzchnię wszystkich figur.
Zadanie 6. (1pkt) Prawda czy fałsz?
Graniastosłup może mieć wysokość poza swoimi konturami.
Graniastosłup może mieć wysokość poza swoimi konturami.
Graniastosłupem jest słynna wieża w Pizie.
Zadanie 7. (1pkt) Prawda czy fałsz?
Jeden litr jest równy 1dm³.
Jeden litr jest równy 1dm³.
To definicja.
Zadanie 8. (1pkt) Prawda czy fałsz?
Zwiększając dwukrotnie wysokość graniastosłupa jednocześnie dwukrotnie zwiększy nam się jego objętość.
Zwiększając dwukrotnie wysokość graniastosłupa jednocześnie dwukrotnie zwiększy nam się jego objętość.
Zwiększamy tylko jedna wielkość.
Zadanie 9. (2pkt) Dzieci narysowały dowolny prostopadłościan i obliczyły jego objętość, po czym narysowały drugi prostopadłościan w skali 2:1. Jaś twierdzi, że objętość drugiego prostopadłościanu będzie dwukrotnie większa od pierwszego. Małgosia uważa, że objętość powinna być ośmiokrotnie większa. Kto ma rację?
To zupełnie inne zadanie jak poprzednio. Zwiększamy trzy wielkości, więc objętość się potęguje.
Zadanie 10. (2pkt) Jaś twierdzi, że znając tylko długość przekątnej podstawy sześcianu jesteśmy w stanie policzyć pole całkowite bryły oraz jej objętość. Małgosia twierdzi, że da się obliczyć tylko jedną z tych rzeczy. Kto ma rację?
Kwadrat jest rombem, wzór na przekątne rombu. Mając pole - wyliczę bok kwadratu.
Zadanie 11. (2pkt) Asia i Monika narysowały w zeszycie graniastosłup prawidłowy trójkątny, którego krawędź podstawy jest równa 6cm. Bryły dziewczyn mają jednak zupełnie inne sumy krawędzi - Asi ma 63cm, a Moniki aż 81cm. O ile wyższy jest graniastosłup Moniki względem graniastosłupa Asi?
Interesuje nas suma krawędzi. U góry i na dole jest taka sama. Różnica jest w wysokości.
Zadanie 12. (2pkt) Pole podstawy dolnej graniastosłupa pięciokątnego prawidłowego jest równe 20cm². Jeśli pole całkowite tej bryły jest równe 100cm², to pole ściany bocznej jest równe:
Odejmujemy dwie podstawy od powierzchni całkowitej i dzielimy przez ilość ścian.
Zadanie 13. (2pkt) Do basenu o długości 25m i szerokości 10m wlano 400 tysięcy litrów wody, co stanowi 23 pojemności basenu. Jaka jest głębokość tego basenu?
Na początku warto obliczyć cała pojemność basenu (można na koniec postępując podobnie z wynikiem). 400 000 : 3/2=
Następnie podstawić do wzoru na objętość (dla ułatwienia przyjąć w metrach sześciennych).
Zadanie 14. (2pkt) Dach o powierzchni 100m² został przykryty pokrywą śnieżną, której każdy m³ waży 200kg. Jak gruba jest ta warstwa śniegu, jeśli cały śnieg na dachu waży jedną tonę?
1tona = 1000 kg to 5 m3
Mamy powierzchnię podstawy i objętość, łatwo wyliczyć wysokość.
Do widzenia.












